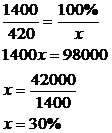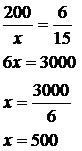LUCRO:CONCEITO E EXEMPLOS

                                     LUCRO

   Suponha que um produto seja adquirido pelo valor PC, e seja vendido pelo valor PV. Isto é:
PC = “preço de custo do produto”
PV = “preço de venda do produto”
L = “lucro obtido com a venda do produto”
Então temos que o lucro obtido com a venda do produto é:

Sendo assim temos:
a) Lucro sobre o preço de custo: .

b) Lucro sobre o preço de venda: .

05. Um comerciante comprou um produto por R$ 400,00 e vendeu por R$ 500,00? Qual foi o lucro sobre o preço de custo?


06. Um comerciante comprou um produto por R$ 400,00 e vendeu por R$ 500,00? Qual foi o lucro sobre o preço de venda?

07. Um produto é comprado por R$ 150,00 e é vendido por R$ 300,00. Qual foi o lucro sobre o preço de custo? Qual foi o lucro sobre o preço de venda?

08. Um produto é vendido com um lucro de 20% sobre o preço de venda. Qual foi o lucro sobre o preço de custo?

DESCONTO SIMPLES-DESCONTO BANCÁRIO:CONCEITO E EXEMPLOS

Desconto Simples Comercial ou Bancário (Por Fora)

    Um dos modelos de juros simples mais utilizados no mercado financeiro é o chamado juro antecipado, juro adiantado, desconto de títulos ou simplesmente desconto bancário. Este é o modelo utilizado na modalidade de desconto e também por empresas de factoring, bem como em transações de curto prazo quando o pagamento for efetuado em uma única parcela, inclusive para cálculo de preço de venda.
Este modelo consiste em calcular o Valor Presente descontando do Valor Futuro (Valor de Face) uma parcela igual ao produto do Valor Futuro pela “taxa de juros” e pelo número de períodos até o vencimento do título negociado. (KUHNEN, 2008).


1.6.1 Fórmulas

Valor do Desconto Simples Comercial


Valor Presente com Desconto Simples Comercial


Valor Futuro com Desconto Simples Comercial
 
 
Número de Períodos com Desconto Simples Comercial
 
 
Taxa de Desconto Simples Comercial
 

 
1 Exemplos

1)   (CRESPO, 2002). Um título de R$ 6.000,00 vai ser descontado à taxa de 2,1% ao mês. Faltando 45 dias para o vencimento do título, determine:
a)   O valor do desconto comercial;
b) O valor atual comercial.

Solução:
a)
 
 
b)
 


2)   (VIEIRA SOBRINHO, 2000). Qual a taxa mensal de desconto utilizada numa operação a 120 dias, cujo valor de resgate é de R$ 1.000,00 e cujo valor atual é de R$ 880,00?

Solução:



3)   (VIEIRA SOBRINHO, 2000). Uma duplicata no valor de R$ 6.800,00 é descontada por um banco, gerando um crédito de R$ 6.000,00 na conta do cliente. Sabendo-se que a taxa cobrada pelo banco é de 3,2% ao mês, determinar o prazo de vencimento da duplicata.

Solução:

 

DESCONTO RACIONAL:CONCEITO E EXEMPLOS

Desconto Racional

    O desconto simple racional (D_r) também chamado de desconto por dentro ou desconto real é equivalente ao juro produzido pelo valor atual do título numa taxa fixada e durante o tempo correspondente.
Na pratica, somente o desconto comercial é utilizado; porém, é necessário fazermos um rápido estudo do desconto racional porque, o desconto composto está ligado a esse conceito. (CRESPO, 2002).


1.7.1 Fórmulas

Valor do Desconto Simples Racional

 

Valor Presente com Desconto Simples Racional

 

Valor Futuro com Desconto Simples Racional

 

Número de Períodos com Desconto Simples Racional

 

Taxa de Desconto Simples Racional
 
  

1.7.2 Exemplos

1)   (ASSAF NETO, 2001). Seja um título de valor nominal de R$ 4.000,00 vencível em um ano, que está sendo liquidado 3 meses antes de seu vencimento. Sendo de 42% a.a. a taxa nominal de juros corrente, pede-se calcular o desconto e o valor descontado desta operação.

Solução:
Desconto
 

Valor Descontado
 


2)   (ASSAF NETO, 2001). Determinar a taxa mensal de desconto racional de um título negociado 60 dias antes de seu vencimento, sendo seu valor de regate igual a R$ 26.000,00 e valor atual na data do desconto de R$ 24.436,10.

Solução:

MONTANTE:CONCEITO E EXEMPLOS

Montante (também conhecido como valor acumulado) é a soma do Capital Inicial com o juro produzido em determinado tempo. Para se chegar a essa conclusão através de uma relação direta pode se fazer uso do seguinte:
P = C + ( t • i • C) onde,
P = Montante
C = Capital
t = tempo de investimento
i = taxa de juro
Observações: Perceba que se a taxa de juros for mensal o tempo deverá ser descrito em meses, e assim por diante, os dois devem estar na mesma unidade de tempo.
Além disso outra informação muito importante e que as vezes passa por despercebido é o a taxa de juros (i) deve estar em forma decimal e não em percentual.

---

Exemplo:

Um Capital (C) de R$20.000 é aplicado durante o período (t) de 6 meses a uma taxa de juros (i) de 10% ao mês, qual o montante ao final do período de investimento?

P = C + ( t • i • C ) =>

P = 20000 + ( 0,10 • 6 • 20000 ) =>

P = 20000 + ( 12000 ) =>

P = 32000

Por tanto, o montante será de R$32.000

---

Perceba que dessa relação que definimos podemos ainda definir o que seria somente o valor ganho no período, basta retirarmos o Capital (C) da adição, assim ficaria:
G = t • i • C onde,
G = Ganho no Período
t = tempo de investimento
i = taxa de juros
C = Capital Investido Capital
O Capital é o valor aplicado através de alguma operação financeira. Também conhecido como: Principal, valor atual, valor presente ou valor

JUROS COMPOSTO:CONCEITO E EXEMPLOS

JUROS COMPOSTO

O atual sistema financeiro utiliza o regime de juros compostos, pois ele oferece uma maior rentabilidade se comparado ao regime de juros simples, onde o valor dos rendimentos se torna fixo, e no caso do composto o juro incide mês a mês de acordo com o somatório acumulativo do capital com o rendimento mensal, isto é, prática do juro sobre juro. As modalidades de investimentos e financiamentos são calculadas de acordo com esse modelo de investimento, pois ele oferece um maior rendimento, originando mais lucro.

Considere que uma pessoa aplique R$ 500,00 durante 8 meses em um banco que paga 1% de juro ao mês. Qual será o valor ao final da aplicação?

A tabela demonstrará mês a mês a movimentação financeira na aplicação do regime de juros compostos.



No final do 8º mês o montante será de R$ 541,43.

Uma expressão matemática utilizada no cálculo dos juros compostos é a seguinte:

M = C * (1 + i)^t, onde:
M: montante
C: capital
i: taxa de juros
t: tempo de aplicação

Obs.: Os cálculos envolvendo juros compostos exigem conhecimentos de manuseio de uma calculadora científica.

Exemplo 2
Qual o montante produzido por um capital de R$ 7.000,00 aplicados a uma taxa de juros mensais de 1,5% durante um ano?

C: R$ 7.000,00
i: 1,5% ao mês = 1,5/100 = 0,015
t: 1 ano = 12 meses

M = C * (1 + i)^t
M = 7000 * (1 + 0,015)¹²
M = 7000 * (1,015)¹²
M = 7000 * 1,195618
M = 8369,33
O montante será de R$ 8.369,33.

Com a utilização dessa fórmula podemos também calcular o capital de acordo com o montante.

Exemplo 3
Calcule o valor do capital que, aplicado a uma taxa de 2% ao mês, rendeu em 10 meses a quantia de R$ 15.237,43?

M: R$ 15.237,43
t: 10
i: 2% a.m. = 2/100 = 0,02

M = C * (1 + i)^t
15237,43 = C * (1 + 0,02)¹⁰
15237,43 = C * (1,02)¹⁰
15237,43 = C * 1,218994
C = 15237,43 / 1,218994
C = 12500,00

O capital é de R$ 12.500,00.


Calculando a taxa de juros da aplicação.

Exemplo 4
Qual a taxa de juros empregada sobre o capital de R$ 8.000,00 durante 12 meses que gerou o montante de R$ 10.145,93?

C: R$ 8.000,00
M: R$ 10.145,93
t: 12
i: ?


A taxa de juros da aplicação foi de 2%.


Calculando o tempo da aplicação. (Uso de técnicas de logaritmo)

JUROS SIMPLES :CONCEITO E EXEMPLOS

JUROS SIMPLES

O calculo de juros simples é feito em relação ao capital inicial, período a período. Desse modo, o valor do juro é constante em cada período.

Quando se deposita ou empresta uma certa quantia, denominada capital por um certo tempo, recebe-se como compensação outra quantia , chamada juros.

Capital __c___ (quantia emprestada)
Taxa____ i___ (porcentagem envolvida)
Tempo___t___ (período do empréstimo)
Juros____j____(a renda obtida)


Os problemas sobre juros simples podem ser resolvidos por meio de uma regra de três composta. Na pratica são resolvidos através de formula.

Exemplo:
O capital 100 em 1 ano produz i
O capital c em t anos produzira j

Capital______tempo______juros

100_________1____________i
c___________ t____________J

I/j=100/c.1/t

i/j= 100/c.t

100j= c.i.t

j=c.i.t/100



OBESERVAÇÃO

A formula somente é válida quando a taxa e o tempo estiverem numa mesma unidade

Exemplos

Calcular os juros produzidos por um capital de R$ 5.000,00 empregado à taxa de 90% ao ano, durante 2 anos

Solução
J = ?, c = 5000, i = 90% ao ano, t = 2 anos

Temos: j = (c.i.t) / 100
Substituindo temos:

J = (5000.90.2) / 100
J = 900000/ 100
J = 9000

Exemplo “2”

Calcular os juros produzidos por um capital de R$ 10.000,00 empregado à taxa de 3% ao mês, durante um ano.

Temos: j = (c . i . t) / 100

J= (10000.3.12) / 100
J = 360000 / 100
J = 3600

Exemplo “3”

Qual o capital que, em quatro meses, rendeu R$ 11.520,00 de juros à taxa de 96% ao ano?

Temos : j = (c.i.t) / 100

11520 = (c.8.4) / 100
32c = 1152000
c = 1152000 / 32
c = 36000

Exemplo “4”

Durante quanto tempo ficou empregado um capital de R$ 45.000,00 que rendeu R$ 8.100,00 de juros, à taxa de 2% ao mês?

Temos : j = (c.i.t) / 100

8100 = (45000. 2. t) / 100
90000t = 810000
t = 810000 / 90000
t = 9

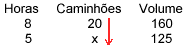
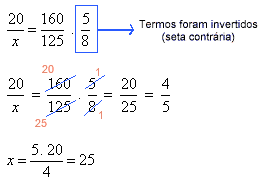
PORCENTAGEM:CONCEITO COM EXEMPLOS

A porcentagem é muito utilizada no mercado financeiro, seja na hora de obter um desconto, calcular o lucro na venda de um produto ou medir as taxas de juros. Na Engenharia, por exemplo, a porcentagem pode ser utilizada para definir o quanto já foi construído de um prédio. Em Administração, pode ser usada para medir as quotas de participação dos sócios em um negócio e por aí vai.

O cálculo percentual nada mais é que a multiplicação de um valor qualquer pelo percentual desejado.


Exemplo 1:

Carlos jogou fora 20% das 10 laranjas que ele tinha. Quantas laranjas foram pro lixo?

10 x 20/100 (vinte por cento) = 2 laranjas

Portanto, 2 laranjas foram jogadas fora por Carlos.

Exemplo 2:

Luana comprou uma cafeteira por R$200,00 e meses depois vendeu por R$300,00. Qual foi a porcentagem (p) de ganho de Luana?

200 + 200 * p/100 = 300
200 * p/100 = 100
p/100 = 100/200
p/100 = 1/2
p= 50

Logo, Luana ganhou 50% na venda da cafeteira

Exemplo 3:

José comprou um computador por R$1000,00 e 2 anos depois o computador foi vendido por R$800,00. De quanto foi a desvalorização (d) do computador?

1000 + 1000 * d/100 = 800
1000 * d/100 = -200
d/100 = 200/1000
d = -20

Logo, José teve um prejuizo de 20% ao comercializar seu computador.

OBSERVAÇAO:

Uma boa dica para entender melhor porcentagem é saber utilizar o Fator de multiplicação.

Fator de multiplicação pode ser um acréscimo ou um decréscimo no valor do produto.

Se um produto aumentou 10% então seu fator de multiplicação é de 1 + taxa de acréscimo, sendo essa taxa de 0,1. Portanto, seu fator de multiplicação é de 1,1.

Se um produto teve um desconto de 10% então seu fator de multiplicação é de 1 - taxa de decréscimo, sendo essa taxa de 0,1. Portanto, seu fator de multiplicaçao é de 0,9.

REGRA DE TRES COMPOSTA:CONCEITO COM EXEMPLOS.

Regra de três composta

A regra de três composta é utilizada em problemas com mais de duas grandezas, direta ou inversamente proporcionais.
        Exemplos:
        1) Em 8 horas, 20 caminhões descarregam 160m³ de areia. Em 5 horas, quantos caminhões serão necessários para descarregar 125m³?
        Solução: montando a tabela, colocando em cada coluna as grandezas de mesma espécie e, em cada linha, as grandezas de espécies diferentes que se correspondem:

Horas	Caminhões	Volume
8	20	160
5	x	125

        Identificação dos tipos de relação:
        Inicialmente colocamos uma seta para baixo na coluna que contém o x (2ª coluna).

        A seguir, devemos comparar cada grandeza com aquela onde está o x.
        Observe que:
        Aumentando o número de horas de trabalho, podemos diminuir o número de caminhões. Portanto a relação é inversamente proporcional (seta para cima na 1ª coluna).

        Aumentando o volume de areia, devemos aumentar o número de caminhões. Portanto a relação é diretamente proporcional (seta para baixo na 3ª coluna). Devemos igualar a razão que contém o termo x com o produto das outras razões de acordo com o sentido das setas.

Montando a proporção e resolvendo a equação temos:

Logo, serão necessários 25 caminhões.

---

        2) Numa fábrica de brinquedos, 8 homens montam 20 carrinhos em 5 dias. Quantos carrinhos serão montados por 4 homens em 16 dias?
        Solução: montando a tabela:

Homens	Carrinhos	Dias
8	20	5
4	x	16

        Observe que:
        Aumentando o número de homens, a produção de carrinhos aumenta. Portanto a relação é diretamente proporcional (não precisamos inverter a razão).

        Aumentando o número de dias, a produção de carrinhos aumenta. Portanto a relação também é diretamente proporcional (não precisamos inverter a razão). Devemos igualar a razão que contém o termo x com o produto das outras razões.

Montando a proporção e resolvendo a equação temos:

Logo, serão montados 32 carrinhos.

---

        3) Dois pedreiros levam 9 dias para construir um muro com 2m de altura. Trabalhando 3 pedreiros e aumentando a altura para 4m, qual será o tempo necessário para completar esse muro?
        Inicialmente colocamos uma seta para baixo na coluna que contém o x. Depois colocam-se flechas concordantes para as grandezas diretamente proporcionais com a incógnita e discordantes para as inversamente proporcionais, como mostra a figura abaixo:

Montando a proporção e resolvendo a equação temos:

Logo, para completar o muro serão necessários 12 dias.

REGRA DE TRÊS SIMPLES:CONCEITO COM EXEMPLOS

Regra de três simples 

 

Regra de três simples com grandezas diretamente proporcionais

A regra de três simples relaciona duas grandezas diferentes através de uma proporcionalidade entre elas. Temos duas possibilidades para essa proporcionalidade entre as grandezas: Grandezas Diretamente Proporcionais  E Grandezas Inversamente Proporcionais. Veremos como realizar os cálculos utilizando a regra de três simples de grandezas que são diretamente proporcionais.
Na regra de três simples, teremos 2 valores para cada grandeza, totalizando 4 valores, entretanto um destes será determinado pelos cálculos que são feitos na regra de três. Apesar de se tratar de simples cálculos a regra de três possui vasta aplicabilidade, desde situações reais de nosso cotidiano até conceitos científicos da Física e Química.
Para que a regra de três seja aplicada com sucesso é de fundamental importância analisar a relação das grandezas e determinar se são diretamente ou inversamente proporcionais, pois isto garante o sucesso deste procedimento.
Vejamos alguns exemplos:
1) Pedro precisa ler alguns livros para o vestibular, e notou que em 3 horas de leitura conseguiu ler 70 páginas. Caso ele mantenha este mesmo ritmo, quantas páginas ele conseguirá ler em um período de 6 horas?

Devemos analisar as grandezas. Se eu leio por uma quantidade maior de tempo, certamente aumentarei a quantidade de páginas lidas, portanto são grandezas diretamente proporcionais, sendo assim não precisamos inverter nenhuma das razões.
Veja que a incógnita x, corresponde a grandeza da quantidade de páginas, portanto durante 6 horas Pedro conseguirá ler 140 páginas.

2) Robson deseja reformar a cozinha de sua casa e foi até a loja de materiais de construção que comprou o material para a reforma do seu banheiro. Ele notou que o azulejo está o mesmo preço de quando ele reformou o banheiro, sabendo que o banheiro dele mede 3metros de largura e 4metros de comprimento e que o total gasto foi de R$150 reais em azulejos, quanto ele gastará para colocar o mesmo tipo de azulejo na sua cozinha que possui as seguintes medidas: 5 metros de largura e 6 metros de comprimento.
Devemos analisar se as grandezas são diretamente ou inversamente proporcionais. Temos duas grandezas: Área a ser revestida pelo azulejo e Dinheiro gasto para compra do azulejo. Fica evidente que se formos revestir uma área maior, iremos gastar maior quantidade de azulejo que por sua vez levará em um maior gasto financeiro. Portanto as duas grandezas são diretamente proporcionais.

GRANDEZAS INVERSAMENTE PROPORCIONAIS:CONCEITO COM EXEMPLOS

Grandezas Inversamente Proporcionais

 

A velocidade é um tipo de grandeza

 Tudo aquilo que pode ser medido ou contado é considerado uma grandeza. Podemos considerar como grandeza as circunstâncias que evolvem comprimento, tempo, temperatura, massa, preço, idade e etc. Entendemos por grandezas inversamente proporcionais as situações onde ocorrem operações inversas, isto é, se dobramos uma grandeza, a outra é reduzida à metade. Um exemplo típico de grandezas inversas são o tempo e a velocidade. Observe o exemplo a seguir:

A distância entre duas cidades é de aproximadamente 200 km. Um veículo com velocidade média de 50 km/h gastou 4 horas para fazer esse percurso. Caso ele dobrasse a velocidade, o tempo gasto seria de 2 horas. Nesse caso observamos que ao aumentar a velocidade do automóvel, o tempo da viagem diminui. Veja a tabela: 

Isso acontece porque velocidade e tempo são inversamente proporcionais.


Exemplo 2

Para encher um tanque são necessárias 60 vasilhas de 6 litros cada uma. Se forem usadas vasilhas de 2 litros cada uma, quantas serão necessárias?




A capacidade da vasilha foi diminuída três vezes, dessa forma, necessitaremos de 180 vasilhas. Portanto, as grandezas vasilhas e capacidade da vasilha são inversamente proporcionais, pois à medida que a capacidade diminui, o número de vasilhas aumenta.

Exemplo 3

Pedro deseja realizar sua festa de aniversário e para isso irá comprar 20 latas de refrigerante com capacidade de 200 ml cada uma, no intuito de evitar desperdício. Caso ele opte por comprar latas de 600 ml, quantas ele deverá comprar? 

Observe que ele irá comprar 30 latas de 200 ml cada, resultando em 6000 ml (6 litros). Caso a capacidade da lata aumente, ele deverá comprar uma quantidade menor de latas afim de não ultrapassar os 6 litros previstos. A capacidade da lata aumentou em três vezes e a quantidade de lata foi dividida por três, constituindo grandezas inversamente proporcionais.

GRANDEZAS DIRETAMENTE PROPORCIONAIS:CONCEITO ECOM EXEMPLOS

Grandezas Diretamente Proporcionais

Cálculo das proporções

A definição de grandeza está associada a tudo aquilo que pode ser medido ou contado. Como exemplo citamos: comprimento, tempo, temperatura, massa, preço, idade e etc.
As grandezas diretamente proporcionais estão ligadas de modo que à medida que uma grandeza aumenta ou diminui, a outra altera de forma proporcional.
Para o melhor entendimento vamos citar alguns exemplos básicos.

Exemplo 1

Uma costureira gasta 1,40 metros de tecido na confecção de uma bermuda. Caso ela queira confeccionar cinco bermudas, quantos metros de tecido serão gastos?
Resolução:
A situação é um típico problema envolvendo grandezas diretamente proporcionais. A costureira irá gastar 7 metros de tecido, pois 1,40 x 5 = 7. À medida que o número de bermudas aumenta, a quantidade de tecido aumenta de forma diretamente proporcional.


Exemplo 2

Um automóvel percorre 300 km com 25 litros de combustível. Caso o proprietário desse automóvel queira percorrer 120 km, quantos litros de combustível serão gastos?
Resolução:
Vamos estabelecer uma ordem de raciocínio lógico calculando quantos quilômetros este veículo percorre com exatamente 1 litro de combustível. Para isso basta dividirmos 300 por 25, que resulta em 12 km por litro.
Agora basta dividir 120 km por 12 km, resultando em 10 litros, que é a quantidade de combustível necessária para percorrer 120 km.

Observe a ideia de grandeza diretamente proporcional: se aumentamos o percurso gastamos mais combustível, isso implica em dizer que, se diminuímos o percurso gastamos menos combustível.


Exemplo 3

Em uma gráfica, certa impressora imprime 100 folhas em 5 minutos. Quantos minutos ela gastará para imprimir 1000 folhas?
Resolução:
A tabela abaixo pode ser construída a fim de relacionar as grandezas folhas e minutos, auxiliando nos cálculos.

Folhas	Minutos
100	5
x10	x10
1000	50

De acordo com a tabela percebemos que o tempo gasto para imprimir 1000 folhas é de 50 minutos, pois ao multiplicar o número de folhas por 10 devemos multiplicar o tempo por 10. Isso ocorre porque as grandezas são diretamente proporcionais.

PROPORÇÃO:CONCEITO E EXEMPLOS

Proporção

 

Proporção

Podemos definir proporção como a igualdade entre duas razões. As proporções são muito utilizadas nas situações envolvendo proporcionalidade direta ou inversa. Para determinarmos se duas razões são proporcionais podemos aplicar a regra fundamental das proporções, que diz: “o produto dos extremos é igual ao produto dos meios”. Veja:

Exemplo 1
Determine o valor de x na proporção a seguir.

Exemplo 2
Calcule o valor de x na proporção .

3*(4x – 2) = 4*(2x – 1)
12x – 6 = 8x – 4
12x – 8x = – 4 + 6
4x = 2
x = 2/4
x = 1/2


A proporção também é muito utilizada nas situações envolvendo porcentagem.
Exemplo 3
Um fogão que custava R$ 1 400,00 estava sendo vendido em uma promoção por
R$ 980,00. Qual era o desconto em porcentagem?

Resolução:
Valor do desconto: 1400 – 980 = 420

O desconto corresponde a 30%.

As proporções constituem a base dos cálculos envolvendo regra de três simples e composta. Observe um exemplo de proporção na resolução da seguinte situação problema utilizando regra de três.

Exemplo 4
Para cada 6 automóveis que vende, Pedro ganha R$ 200,00 de comissão. Quanto ele recebeu de comissão no mês em que vendeu 15 automóveis?

 

comissão (R$)	automóveis
200	6
x	15

No mês em que ele vendeu 15 carros recebeu uma comissão de R$ 500,00.

Proporção

Podemos definir proporção como a igualdade entre duas razões. As proporções são muito utilizadas nas situações envolvendo proporcionalidade direta ou inversa. Para determinarmos se duas razões são proporcionais podemos aplicar a regra fundamental das proporções, que diz: “o produto dos extremos é igual ao produto dos meios”. Veja:

Exemplo 1
Determine o valor de x na proporção a seguir.

Exemplo 2
Calcule o valor de x na proporção .

3*(4x – 2) = 4*(2x – 1)
12x – 6 = 8x – 4
12x – 8x = – 4 + 6
4x = 2
x = 2/4
x = 1/2


A proporção também é muito utilizada nas situações envolvendo porcentagem.
Exemplo 3
Um fogão que custava R$ 1 400,00 estava sendo vendido em uma promoção por
R$ 980,00. Qual era o desconto em porcentagem?

Resolução:
Valor do desconto: 1400 – 980 = 420

O desconto corresponde a 30%.

As proporções constituem a base dos cálculos envolvendo regra de três simples e composta. Observe um exemplo de proporção na resolução da seguinte situação problema utilizando regra de três.

Exemplo 4
Para cada 6 automóveis que vende, Pedro ganha R$ 200,00 de comissão. Quanto ele recebeu de comissão no mês em que vendeu 15 automóveis?

 

comissão (R$)	automóveis
200	6
x	15

No mês em que ele vendeu 15 carros recebeu uma comissão de R$ 500,00.